1. 최소 신장 트리(최소 스패닝 트리 ; Minimum Spanning Tree)
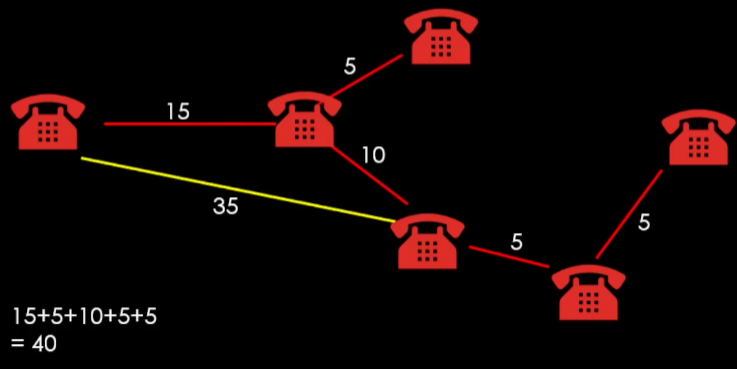
최소한의 간선을 이용하여 모든 정점을 연결한 트리.
(1) 순환이 발생하면 안됨
ex) 0 -> 1 -> 2 -> 0 -> 1 ...
(2) 정점이 N개이면 간선은 N-1개
2. 크루스칼 알고리즘 (Kruskal MST Algorithm)
탐욕적인(greedy) 방법을 이용함.
-> 지금 순간에 최적인 답을 선택하여 결과를 도출
- 원리
(1) 코스트가 가장 낮은 간선들을 선택
(2) 코스트가 가장 낮은 다른 간선을 연결
(3) 그 다음으로 코스트가 낮은 간선을 연결 반복
단, 연결 사이에 순환이 발생하면 안됨(MST의 조건에 미달)
- 순환을 판단하는 방법
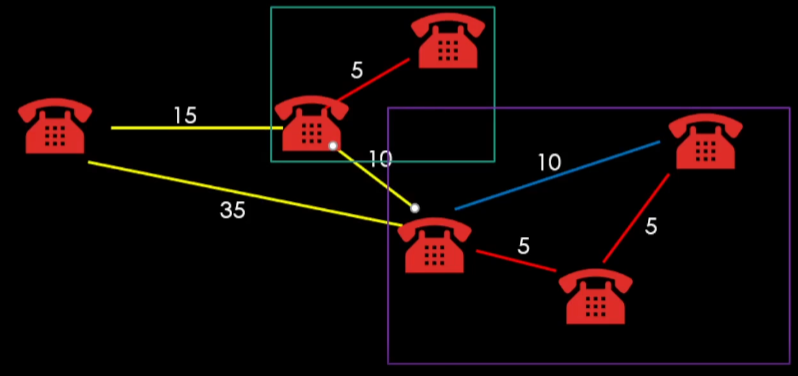
연결이 완료된 정점들을 그룹으로 관리한다.
이 때 같은 그룹내에서 정점과 정점을 새로운 간선으로 추가하면 순환이 발생한다.
(다른 그룹과의 연결은 순환이 아니다)
다른 그룹과 연결되면 하나의 그룹으로 통합한다.
<- 유니온-파인드 알고리즘 사용
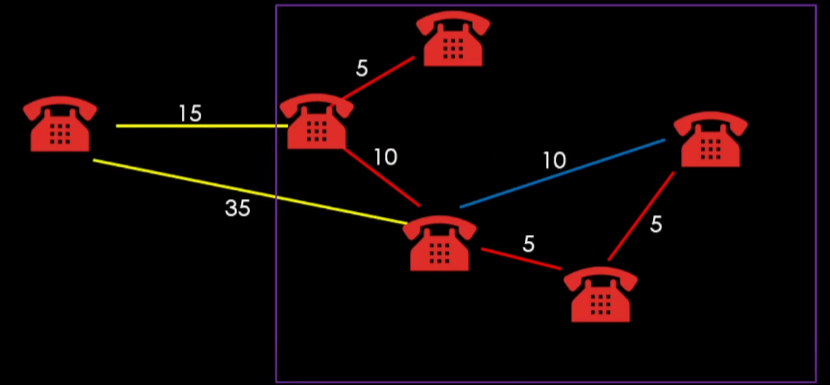
3. 코드 분석
이전 글에서 작성한 DisjointSet class를 그대로 사용한다.
6-1. 상호 배타적 집합 (Disjoint Set)
최소 스패닝 트리를 공부하기 전에, 최소 스패닝 트리에 적용되는 서로소 집합에 대해서 공부한다. 1. 상호 배타적 집합(서로소 집합) ; Disjoint Set - 공통 원소(혹은 공통 부분 집합)를 가지지 않는
crat.tistory.com
(1) 그래프 구현하기
struct Vertex
{
// data
};
vector<Vertex> vertices;
vector<vector<int>> adjacent;
void CreateGraph()
{
vertices.resize(6); // 6개의 정점 사용
adjacent = vector<vector<int>>(6, vector<int>(6, -1)); // 이중 배열,
adjacent[0][1] = adjacent[1][0] = 15;
adjacent[0][3] = adjacent[3][0] = 35;
adjacent[1][2] = adjacent[2][1] = 5;
adjacent[1][3] = adjacent[3][1] = 10;
adjacent[3][4] = adjacent[4][3] = 5;
adjacent[3][5] = adjacent[5][3] = 10;
adjacent[5][4] = adjacent[4][5] = 5;
}위 그림을 보고 정점과 그래프를 구현한다.
vertices는 각 정점을, adjacent는 각 간선들의 연결을 나타낸다.
여기에서 adjacent는 이중배열이며 모든 요소가 -1로 초기화 되어 있다.
(2) 경로의 코스트를 저장하는 구조체
struct CostEdge // u에서 v까지 코스트
{
int cost;
int u;
int v;
bool operator<(CostEdge& other)
{
return cost < other.cost;
}
};정점 u에서 정점 v 까지의 코스트를 cost에 저장하는 구조체이다.
아래에 작성된 Kruskal 함수에서 쓰인다.
4. Kruskal 알고리즘
(1) 이중 반복문
int Kruskal(vector<CostEdge>& selected) // 계산한 코스트를 반환
{
int ret = 0;
selected.clear();
vector<CostEdge> edges;
for (int u = 0; u < adjacent.size(); u++)
{
for (int v = 0; v < adjacent[u].size(); v++)
{
// 간선이 중복되지 않게 한다
if (u > v)
continue;
int cost = adjacent[u][v];
if (cost == -1)
continue;
edges.push_back(CostEdge{ cost, u, v });
}
}
std::sort(edges.begin(), edges.end());
결과값을 반환할 ret 변수를 0으로 초기화한다.
알고리즘에 의해 코스트가 가장 낮은 간선들이 edges 배열에 push_back 된다.
이 때 adjacent 이중 배열이 양방향 연결로 되어있기 때문에, if 문을 통해서 중복을 방지한다.
또한 정점 간 연결이 되어있지 않으면(cost = -1) continue로 함수를 빠져나온다.
이후에 sort를 사용하여 오름차순으로 정렬한다(큰 값이 배열의 가장 오른쪽에 있다).
(2) 그룹 구성하기
// 그룹 구성
DisjointSet sets(vertices.size());
for (CostEdge& edge : edges)
{
// 순환을 회피하기 위해 같은 그룹이면 스킵
if (sets.Find(edge.u) == sets.Find(edge.v))
continue;
// 하나의 그룹으로 합침
sets.Merge(edge.u, edge.v);
selected.push_back(edge);
ret += edge.cost;
}
// 코스트가 가장 낮은 정점을 선택
return ret;
}사전에 사용했던 DisjointSet class를 이용하여 정점들을 그룹화한다.
그리고 정렬되어 있는 edges 배열의 각 요소를 순회한다.
edge의 u와 v가 속한 그룹의 루트 노드를 비교하여 서로 같다면(같은 그룹내에 있다면) 함수를 빠져나온다.
그렇지 않다면 그룹을 하나로 합친다.
처음 입력받았던 배열인 selected에 순회중인 edges의 각 정점들(edge)을 하나씩 밀어넣는다.
그리고 ret에 코스트를 더해 최종적인 코스트를 반환한다.
(3) main
int main()
{
CreateGraph();
vector<CostEdge> selected;
int cost = Kruskal(selected);
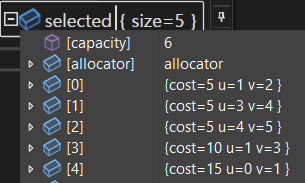
}중지점을 걸어 확인하면 아래와 같이 최종 코스트와 Kruskal 알고리즘에 따라 선택된 간선을 확인할 수 있다.
'자료구조와 알고리즘 > 탐색 트리 & 최소 스패닝 트리' 카테고리의 다른 글
| 6-1. 상호 배타적 집합 (Disjoint Set) (0) | 2023.07.20 |
|---|---|
| 4-5. 레드-블랙 트리(RBT ; Red-Black Tree) - (3) 데이터 삭제 구현 (0) | 2023.07.18 |
| 4-4. 레드-블랙 트리(RBT ; Red-Black Tree) - (2) 데이터 삭제 (0) | 2023.07.18 |
| 4-3. 레드-블랙 트리(RBT ; Red-Black Tree) - (1) (0) | 2023.07.18 |
| 4-2. 이진 탐색 트리(BST ; Binary Search Tree) (0) | 2023.07.14 |
