0. 이진 탐색 트리의 문제점
이진 탐색 트리는 균형이 한 쪽으로 무너지면 속도에서의 이점이 사라지게 된다.
레드-블랙 트리는 균형을 맞추기 위해 색 변경, 노드 회전(부모 - 자식 위치 변경)의 과정을 거친다.
1. 레드-블랙 트리(Red-Black Tree)의 특징

이진 탐색 트리를 기반으로 한다.
(1) 모든 노드는 블랙 또는 레드 중 하나이다.
(2) 루트 노드는 블랙이다.
(3) 모든 리프 노드는 블랙이다.
(4) 레드 노드의 자식 노드 양쪽은 언제나 블랙이다.
(레드 노드는 연속적으로 있을 수 없다 -> 레드 노드의 부모와 자식은 블랙이어야 한다)
(5) 어떤 노드에서 하위 리프 노드로 가는 모든 경로에는 (리프 노드를 제외하고) 모두 같은 개수의 블랙 노드가 있다.
(6) 새로운 노드는 레드이다.
=> 위의 특징들을 만족하지 않을 때 트리를 재구성한다.
2. 기본 구조 구현
BST의 소스를 그대로 이용하여 수정한다.
2023.07.14 - [자료 구조와 알고리즘/탐색 트리] - 4-2. 이진 탐색 트리(BST ; Binary Search Tree)
(1) 레드, 블랙 색상 추가 (BinarySearchTree.h)
enum class Color
{
Red = 0,
Black = 1,
};레드-블랙 트리의 핵심인 노드의 색을 추가한다.
이후에 노드의 멤버 변수에 color를 추가한다.
struct Node
{
Node* left = nullptr;
Node* right = nullptr;
Node* parent = nullptr;
int key = { }; //data
Color color = Color::Black; // (3) NIL 노드는 블랙
};막 생성된 노드는 블랙으로 생성하게 된다.
(2) Nullptr을 대체할 더미 노드 NIL (BinarySearchTree.h)
private:
Node* _root = nullptr;
Node* _nil = nullptr;
};BinarySearchTree 클래스에 더미 노드 _nil을 추가한다.
나중에 회전 알고리즘에 필요하다.
(3) 기본 생성자와 소멸자 수정 (BinarySearchTree.h, BinarySearchTree.cpp)
class BinarySearchTree
{
public:
BinarySearchTree();
~BinarySearchTree();
// ~~~~~~~
BinarySearchTree::BinarySearchTree()
{
_nil = new Node(); // 초기 상태는 블랙
_root = _nil;
}
BinarySearchTree::~BinarySearchTree()
{
delete _nil;
}노드가 처음 생성되면 nullptr이 아니라 더미 노드로 생성되도록 기본 생성자에 세팅한다.
노드의 처음 색상은 Node 구조체에서 블랙으로 세팅되어있다.
(4) 콘솔 상 노드의 색상 표현을 위한 SetCursorColor (BinarySearchTree.cpp)
2023.06.27 - [자료 구조와 알고리즘/예제] - 1-1. Maze 구현을 위한 환경설정
위 글에서 사용된 SetCursorColor를 (int16 -> SHORT) 사용한다.
enum class ConsoleColor
{
BLACK = 0,
RED = FOREGROUND_RED,
GREEN = FOREGROUND_GREEN,
BLUE = FOREGROUND_BLUE,
YELLOW = RED | GREEN,
WHITE = RED | GREEN | BLUE,
};
void SetCursorColor(ConsoleColor color)
{
HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
::SetConsoleTextAttribute(output, static_cast<SHORT>(color));
}
(5) 새로운 함수 추가 / 사용하지 않는 함수 삭제 (BinarySearchTree.h, BinarySearchTree.cpp)
class BinarySearchTree
{
public:
BinarySearchTree();
~BinarySearchTree();
void Print() { Print(_root, 10, 0); }
void Print(Node* node, int x, int y);
// 데이터 탐색
Node* Search(Node* node, int key);
Node* Min(Node* node);
Node* Max(Node* node);
Node* Next(Node* node);
// 데이터 추가, 삭제
void Insert(int key);
void InsertFixup(Node* node);
void Delete(int key);
void Delete(Node* node);
void Replace(Node* u, Node* v);
void LeftRotate(Node* node);
void RightRotate(Node* node);더 이상 사용하지 않는 PrintInorder 등을 삭제하고, 레드-블랙 트리에서 사용되는 InsertFixup, LeftRotate, RightRotate 함수를 추가한다.
(6) nullptr (BinarySearchTree.cpp)
이제는 nullptr 대신 더미 노드 _nil을 사용하기로 했기 때문에, nullptr을 _nil로 모두 변경해주도록 한다.
또한 아래와 같이 null check를 해주는 부분의 비교식도 모두 수정한다.
Node* BinarySearchTree::Min(Node* node)
{ // 왼쪽에 있는 노드가 더 작다, _nil까지
while (node->left != _nil)
node = node->left;
return node;
}
Node* BinarySearchTree::Max(Node* node)
{ // 오른쪽에 있는 노드가 더 크다, _nil까지
while (node->right != _nil)
node = node->right;
return node;
}
Node* BinarySearchTree::Next(Node* node)
{ // 이 노드 다음으로 큰 노드
if (node->right != _nil) // 서브 노드의 최소값
return Min(node->right);
Node* parent = node->parent;
while (parent != _nil && node == parent->right)
{
//~~~
}
return parent;
}이 뿐만 아니라 while문과 if문에 있는 대부분의 null check를 '!=' (같지 않음 연산자)로 바꿔준다.
3. 코드 설명
#include "BinarySearchTree.h"
#include <iostream>
#include <windows.h>
using namespace std;
enum class ConsoleColor
{
BLACK = 0,
RED = FOREGROUND_RED,
GREEN = FOREGROUND_GREEN,
BLUE = FOREGROUND_BLUE,
YELLOW = RED | GREEN,
WHITE = RED | GREEN | BLUE,
};
void SetCursorColor(ConsoleColor color)
{
HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
::SetConsoleTextAttribute(output, static_cast<SHORT>(color));
}
void SetCursorPosition(int x, int y)
{
HANDLE output = ::GetStdHandle(STD_OUTPUT_HANDLE);
COORD pos = { static_cast<SHORT>(x), static_cast<SHORT>(y) };
::SetConsoleCursorPosition(output, pos);
}
BinarySearchTree::BinarySearchTree()
{
_nil = new Node(); // 초기 상태는 블랙
_root = _nil;
}
BinarySearchTree::~BinarySearchTree()
{
delete _nil;
}
void BinarySearchTree::Print(Node* node, int x, int y)
{
if (node == _nil)
return;
SetCursorPosition(x, y);
if (node->color == Color::Black)
SetCursorColor(ConsoleColor::BLUE);
else
SetCursorColor(ConsoleColor::RED);
cout << node->key;
Print(node->left, x - (5 / (y + 1)), y + 1);
Print(node->right, x + (5 / (y + 1)), y + 1);
SetCursorColor(ConsoleColor::WHITE);
}
Node* BinarySearchTree::Search(Node* node, int key)
{
if (node == _nil || key == node->key)
return node;
// 재귀 함수 구조
if (key < node->key)
return Search(node->left, key);
else
return Search(node->right, key);
}
Node* BinarySearchTree::Min(Node* node)
{ // 왼쪽에 있는 노드가 더 작다, _nil까지
while (node->left != _nil)
node = node->left;
return node;
}
Node* BinarySearchTree::Max(Node* node)
{ // 오른쪽에 있는 노드가 더 크다, _nil까지
while (node->right != _nil)
node = node->right;
return node;
}
Node* BinarySearchTree::Next(Node* node)
{ // 이 노드 다음으로 큰 노드
if (node->right != _nil) // 서브 노드의 최소값
return Min(node->right);
Node* parent = node->parent;
// 부모가 유효하고 이 노드가 부모의 우측에 있다면
while (parent != _nil && node == parent->right)
{ // 위로 역행하며 올라감
node = parent; // 이 노드의 부모로 올라감
parent = parent->parent; // 부모의 부모를 parent로 설정
}
return parent;
}
void BinarySearchTree::Insert(int key)
{
Node* newNode = new Node();
newNode->key = key;
Node* node = _root;
Node* parent = _nil;
while (node != _nil)
{
parent = node; // 초기화
if (key < node->key)
node = node->left;
else
node = node->right;
}
// 부모의 왼쪽 or 오른쪽에 붙임
newNode->parent = parent;
if (parent == _nil)
_root = newNode;
else if (key < parent->key)
parent->left = newNode;
else
parent->right = newNode;
// 검사
newNode->left = _nil;
newNode->right = _nil;
newNode->color = Color::Red;
InsertFixup(newNode);
}
void BinarySearchTree::InsertFixup(Node* node)
{
// 1) parent == red, uncle == red
// -> p = black, u = black, pp =red
// 2) parent == red, uncle == black (triangle)
// -> 회전을 통해 3)으로 만듬
// 3) parent == red, uncle == black (list)
// -> 색상 변경 후 회전
// [pp(B)]
// [p(R)] [u]
// [n(R)] , 색 바꾸기
while (node->parent->color == Color::Red)
{
if (node->parent == node->parent->parent->left)
{
Node* uncle = node->parent->parent->right;
// 삼촌이 레드
if (uncle->color == Color::Red)
{ // 부모, 삼촌 : 블랙, 부모의 부모 : 레드
node->parent->color = Color::Black;
uncle->color = Color::Black;
node->parent->parent->color = Color::Red;
// 2세대 이후를 검증함(거슬러 올라감)
node = node->parent->parent;
}
else // 삼촌이 블랙
{ // triangle : left -> right
// list : left -> left
if (node == node->parent->right)
// Triangle Type ; left rotate
{
node = node->parent;
LeftRotate(node);
}
// List Type
node->parent->color = Color::Black;
node->parent->parent->color = Color::Red;
RightRotate(node->parent->parent);
}
}
else
{
Node* uncle = node->parent->parent->left;
// 삼촌이 레드
if (uncle->color == Color::Red)
{ // 부모, 삼촌 : 블랙, 부모의 부모 : 레드
node->parent->color = Color::Black;
uncle->color = Color::Black;
node->parent->parent->color = Color::Red;
// 2세대 이후를 검증함(거슬러 올라감)
node = node->parent->parent;
}
else // 삼촌이 블랙
{ // triangle : left -> right
// list : left -> left
if (node == node->parent->left)
// Triangle Type ; left rotate
{
node = node->parent;
RightRotate(node);
}
// List Type
node->parent->color = Color::Black;
node->parent->parent->color = Color::Red;
LeftRotate(node->parent->parent);
}
}
}
// 2) 루트는 항상 블랙
_root->color = Color::Black;
}
void BinarySearchTree::Delete(int key)
{
Node* deleteNode = Search(_root, key);
Delete(deleteNode);
}
void BinarySearchTree::Delete(Node* node)
{
if (node == _nil)
return;
if (node->left == _nil) // 자식이 우측에 하나거나 없음
Replace(node, node->right);
else if (node->right == _nil) // 자식이 좌측에 하나거나 없음
Replace(node, node->left);
else
{ // 다음 데이터 찾기
Node* next = Next(node);
node->key = next->key;
Delete(next);
}
}
// u 서브트리를 v 서브트리로 교체
// u를 동적 할당 해제
void BinarySearchTree::Replace(Node* u, Node* v)
{ // 부모에서 자식으로 연결하기
if (u->parent == _nil) // null이면 루트 노드
_root = v;
else if (u == u->parent->left) // 이 노드가 부모 좌측에 위치
u->parent->left = v;
else
u->parent->right = v;
if (v) // 자식에서 부모로 연결하기
v->parent = u->parent;
delete u;
}
void BinarySearchTree::LeftRotate(Node* x)
{
Node* y = x->right;
x->right = y->left; // [2]
if(y->left != _nil)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == _nil)
_root = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}
void BinarySearchTree::RightRotate(Node* y)
{
Node* x = y->left;
y->left = x->right; // [2]
if (y->right != _nil)
y->right->parent = y;
x->parent = y->parent;
if (y->parent == _nil)
_root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
x->right = y;
y->parent = x;
}
(1) Print 함수
void BinarySearchTree::Print(Node* node, int x, int y)
{
if (node == _nil)
return;
SetCursorPosition(x, y);
if (node->color == Color::Black)
SetCursorColor(ConsoleColor::BLUE);
else
SetCursorColor(ConsoleColor::RED);
cout << node->key;
Print(node->left, x - (5 / (y + 1)), y + 1);
Print(node->right, x + (5 / (y + 1)), y + 1);
SetCursorColor(ConsoleColor::WHITE);
}node가 더미 노드라면 print할 필요가 없으므로 함수를 빠져나온다.
노드에 컬러 속성이 포함되었으므로 노드의 기본 컬러가 블랙이면 콘솔 상에서 잘 보이도록 파랑으로 설정한다.
그리고 최하단에 출력이 모두 끝난 이후에 나타나는 안내 문구를 하양으로 나타내도록 변경한다.
(2) Insert 함수
void BinarySearchTree::Insert(int key)
{
Node* newNode = new Node();
newNode->key = key;
Node* node = _root;
Node* parent = _nil;
while (node != _nil)
{
parent = node; // 초기화
if (key < node->key)
node = node->left;
else
node = node->right;
}
// 부모의 왼쪽 or 오른쪽에 붙임
newNode->parent = parent;
if (parent == _nil)
_root = newNode;
else if (key < parent->key)
parent->left = newNode;
else
parent->right = newNode;
// 검사
newNode->left = _nil;
newNode->right = _nil;
newNode->color = Color::Red;
InsertFixup(newNode);
}새로 생성되는 leaf 노드를 부모 노드에 붙이는 작업이다.
이전 코드에서 null check 부분이 수정되었다.
if문 이후에 leaf 노드의 좌, 우측 자식은 더미 노드로 설정한다.
그리고 새로 생성되는 노드의 색상은 레드이다.
(기존 트리를 재구성 하지 않는 방향으로 가기 위해서 레드로 추가한다)
이후에 InsertFixup을 통해서 트리를 재구성한다.
(3) LeftRotate (좌회전, 반시계 방향 회전), RightRotate (우회전, 시계 방향 회전)
트리에 새로운 노드가 추가되었을 때 트리는 모든 조건이 만족되도록 구성되어야 한다.
(1) 모든 노드는 블랙 또는 레드 중 하나이다.
(2) 루트 노드는 블랙이다.
(3) 모든 리프 노드는 블랙이다.
(4) 레드 노드의 자식 노드 양쪽은 언제나 블랙이다.
(레드 노드는 연속적으로 있을 수 없다 -> 레드 노드의 부모와 자식은 블랙이어야 한다)
(5) 어떤 노드에서 하위 리프 노드로 가는 모든 경로에는 (리프 노드를 제외하고) 모두 같은 개수의 블랙 노드가 있다.
(6) 새로운 노드는 레드이다.
(3-1) 좌회전, Left Rotate
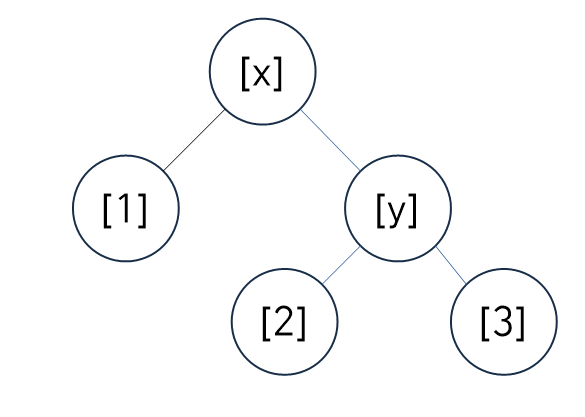
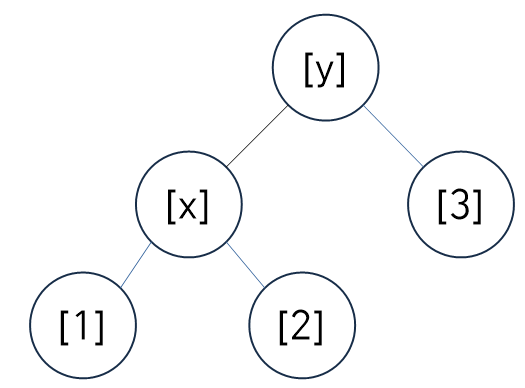
void BinarySearchTree::LeftRotate(Node* x)
{
Node* y = x->right;
x->right = y->left; // [2]
if(y->left != _nil)
y->left->parent = x;
y->parent = x->parent;
if (x->parent == _nil)
_root = y;
else if (x == x->parent->left)
x->parent->left = y;
else
x->parent->right = y;
y->left = x;
x->parent = y;
}기존 구조에서 각 요소를 왼쪽으로 좌회전했다고 생각하자.
먼저 기존 구조의 y를 x의 오른쪽에 있었다고 초기화한다.
그리고 그림에 맞게 노드를 하나씩 회전시켜준다.
이 때 기준 노드(Node 타입의 x 노드)의 부모가 없다면 최상위 노드라는 뜻이므로, 단순히 root 노드에 y를 대입시키면 된다.
그리고 x의 위치가 부모의 좌측인지 우측인지 확인 후에 y 노드와 바꿔준다.
이후에 끊어진 x와 y를 연결해주면 된다.
(3-2) 우회전, Right Rotate


void BinarySearchTree::RightRotate(Node* y)
{
Node* x = y->left;
y->left = x->right; // [2]
if (y->right != _nil)
y->right->parent = y;
x->parent = y->parent;
if (y->parent == _nil)
_root = x;
else if (y == y->parent->left)
y->parent->left = x;
else
y->parent->right = x;
x->right = y;
y->parent = x;
}RightRotate는 LeftRotate의 대칭적인 형태를 띤다.
LeftRotate의 y를 x로, x를 y로 바꾼 후에 right를 left로, left를 right로 변경한다.
(4) InsertFixup 함수
(1) 모든 노드는 블랙 또는 레드 중 하나이다.
(2) 루트 노드는 블랙이다.
(3) 모든 리프 노드는 블랙이다.
(4) 레드 노드의 자식 노드 양쪽은 언제나 블랙이다.
(레드 노드는 연속적으로 있을 수 없다 -> 레드 노드의 부모와 자식은 블랙이어야 한다)
(5) 어떤 노드에서 하위 리프 노드로 가는 모든 경로에는 (리프 노드를 제외하고) 모두 같은 개수의 블랙 노드가 있다.
(6) 새로운 노드는 레드이다.
자신과 부모 노드가 레드일 때, 삼촌(uncle) 노드의 색에 따라서 두 가지 방법을 택한다.
(4-1) 삼촌 노드가 부모-부모 노드의 우측 && 삼촌 노드의 색이 Red일 때
void BinarySearchTree::InsertFixup(Node* node)
{
// 1) parent == red, uncle == red
// -> p = black, u = black, pp =red
// 2) parent == red, uncle == black (triangle)
// -> 회전을 통해 3)으로 만듬
// 3) parent == red, uncle == black (list)
// -> 색상 변경 후 회전
// [pp(B)]
// [p(R)] [u]
// [n(R)] , 색 바꾸기
while (node->parent->color == Color::Red)
{
if (node->parent == node->parent->parent->left)
{
Node* uncle = node->parent->parent->right;
// 삼촌이 레드
if (uncle->color == Color::Red)
{ // 부모, 삼촌 : 블랙, 부모의 부모 : 레드
node->parent->color = Color::Black;
uncle->color = Color::Black;
node->parent->parent->color = Color::Red;
// 2세대 이후를 검증함(거슬러 올라감)
node = node->parent->parent;
}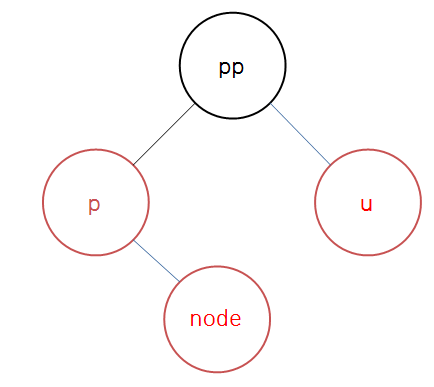
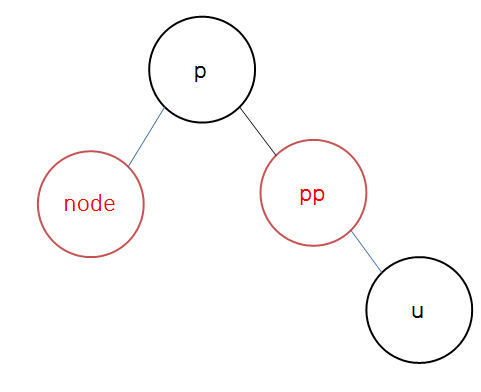
leaf 노드가 부모의 우측에 있어서, 부모의 부모 - 부모 - 자식으로 이어지는 형태가 삼각형의 모양을 띤다.
레드 - 레드는 연속으로 있으면 안되므로, 부모와 삼촌 노드의 색을 Black, 부모의 부모(pp)를 Red로 변경하면 된다.
그리고 2세대 이후를 거슬러 올라가며 검증한다(node = node->parent->parent).
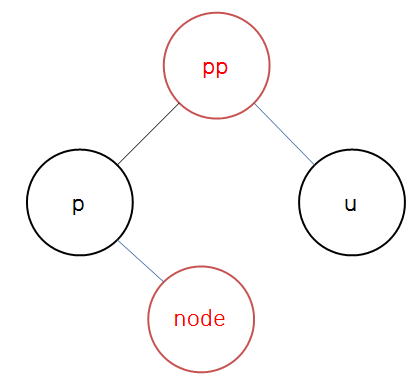
이후에는 공통적으로 적용되는 코드로 노드의 부모(p)와 부모의 부모(pp)의 색을 다시 한번 올바르게 적용하고, 부모의 부모를 기준으로 오른쪽 회전한다.
(4-2) 삼촌 노드가 부모-부모 노드의 우측 && 삼촌 노드의 색이 Black일 때
{ // triangle : left -> right
// list : left -> left
if (node == node->parent->right)
// Triangle Type ; left rotate
{
node = node->parent;
LeftRotate(node);
}
// List Type
node->parent->color = Color::Black;
node->parent->parent->color = Color::Red;
RightRotate(node->parent->parent);
}
}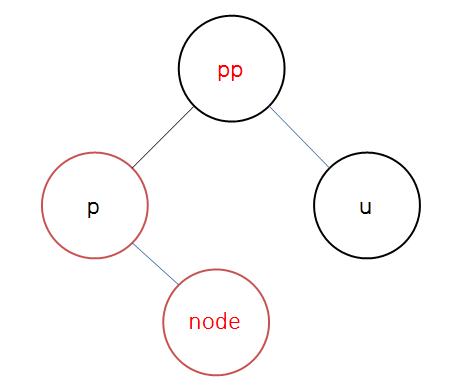
레드-블랙 트리의 이진 탐색 트리적 특성을 유지하기 위해서(작은 값이 왼쪽으로 오도록)
노드가 부모의 오른쪽에 있으면 부모를 기준으로(노드의 부모를 노드로 설정) 왼쪽 회전을 실행하여 노드의 위치를 바꿔줘야 한다.
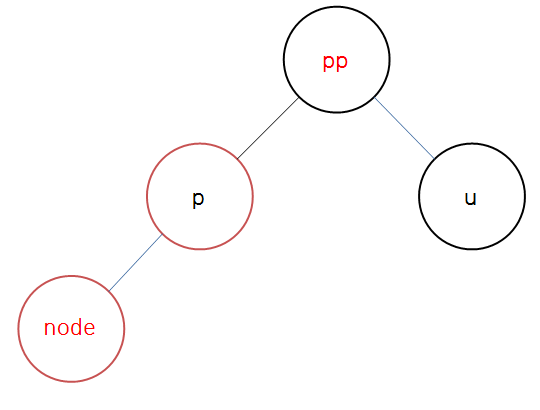
이후에는 공통적으로 적용되는 코드로 노드의 부모(p)와 부모의 부모(pp)의 색을 다시 한번 올바르게 적용하고, 부모의 부모를 기준으로 오른쪽 회전한다.
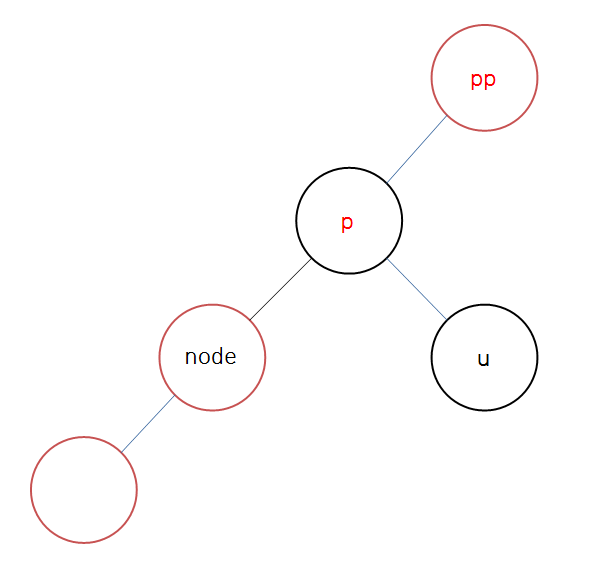
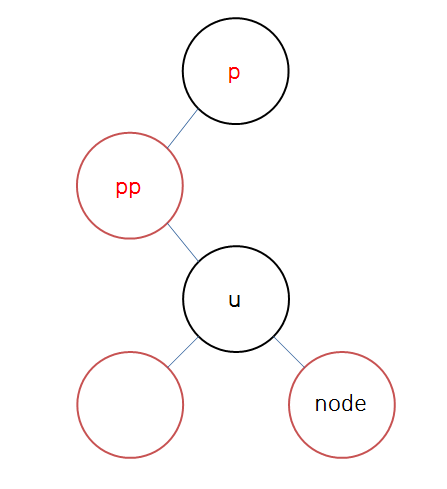
(4-3) 삼촌 노드가 부모-부모 노드의 좌측 && 삼촌 노드의 색이 Red일 때
else
{
Node* uncle = node->parent->parent->left;
// 삼촌이 레드
if (uncle->color == Color::Red)
{ // 부모, 삼촌 : 블랙, 부모의 부모 : 레드
node->parent->color = Color::Black;
uncle->color = Color::Black;
node->parent->parent->color = Color::Red;
// 2세대 이후를 검증함(거슬러 올라감)
node = node->parent->parent;
}(4-1)번의 코드와 동일하지만 대신 우회전을 시켜준다.
(4-4) 삼촌 노드가 부모-부모 노드의 좌측 && 삼촌 노드의 색이 Black일 때
else // 삼촌이 블랙
{ // triangle : left -> right
// list : left -> left
if (node == node->parent->left)
// Triangle Type ; left rotate
{
node = node->parent;
RightRotate(node);
}
// List Type
node->parent->color = Color::Black;
node->parent->parent->color = Color::Red;
LeftRotate(node->parent->parent);
}
}
}
// 2) 루트는 항상 블랙
_root->color = Color::Black;
}(4-2)번의 코드와 동일하지만 대신 좌회전을 시켜준다.
'자료구조와 알고리즘 > 탐색 트리 & 최소 스패닝 트리' 카테고리의 다른 글
| 6-1. 상호 배타적 집합 (Disjoint Set) (0) | 2023.07.20 |
|---|---|
| 4-5. 레드-블랙 트리(RBT ; Red-Black Tree) - (3) 데이터 삭제 구현 (0) | 2023.07.18 |
| 4-4. 레드-블랙 트리(RBT ; Red-Black Tree) - (2) 데이터 삭제 (0) | 2023.07.18 |
| 4-2. 이진 탐색 트리(BST ; Binary Search Tree) (0) | 2023.07.14 |
| 4-1. 이진 탐색(Binary Search) (0) | 2023.07.13 |

