0. vs Kruskal
크루스칼 알고리즘은 탐욕적인 방법을 이용하여 가장 작은 간선을 먼저 선택하는 방법을 이용하여
그룹을 합치고 경로를 발견했다.
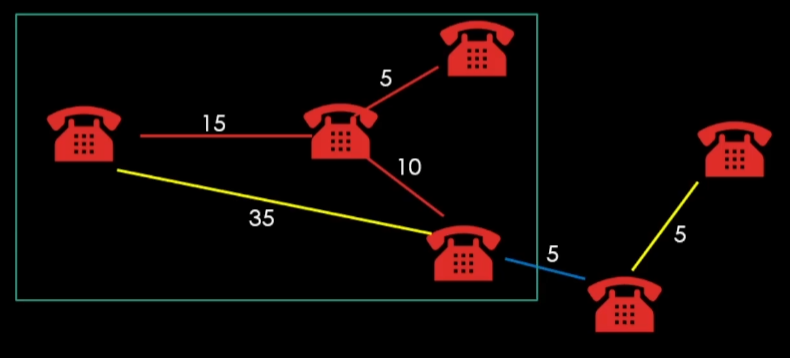
프림 알고리즘은 랜덤의 정점을 기준으로 간선을 하나씩 수집하여 진행한다.
(정점에서 이어진 간선들 중 최적의 간선을 선택)
그리고 간선으로 연결된 정점과 그룹화한다.
이 때 다음 간선을 확인하고 이전의 간선들과 비교했을 때, 다음 간선이 이전의 간선보다 훨씬 낮으므로
이전의 쓸모없는 간선은 사용하지 않는다.
(위 그림에서 35에 해당하는 간선)

- 다익스트라 알고리즘과는 다른점?
다익스트라는 시작점을 기준으로 코스트가 낮은 간선을 선택하지만
프림은 트리(정점 집합)을 기준으로 코스트가 낮은 간선을 선택한다.
1. 코드 수정
2023.07.25 - [자료 구조와 알고리즘/예제] - 6-3. 크루스칼 알고리즘을 활용한 미로 맵 만들기
6-3. 크루스칼 알고리즘을 활용한 미로 맵 만들기
0. 구상 사전에 사용했던 미로 맵을 Kruskal 알고리즘을 사용하여 만든다. (기존의 미로 맵은 탈출구가 있던 세로 줄과 가로 줄은 모두 초록색으로 길이 뚫려 있었다) 간선을 경로로 만들고, 코스트
crat.tistory.com
기존의 GenerateMap은 GenerateMap_Kruskal로 변경한다.
이어 Player.cpp 내의 GenerateMap_Kruskal을 GenerateMap_Prim으로,
Board.cpp 내에서 GenerateMap_Kruskal을 이용하여 맵을 생성하는 코드를 찾아 GenerateMap_Prim으로 수정해준다.
Board.h의 CostEdge 구조체는 GenerateMap_Kruskal 함수 내로 이동시킨다.
2. 코드 분석
void Board::GenerateMap_Prim()
{
struct CostEdge
{
int cost;
Pos vtx; // 좌표를 가지는 노드
bool operator<(const CostEdge& other) const
{
return cost < other.cost;
}
};
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{
if (x % 2 == 0 || y % 2 == 0) // 첫번째 가로줄과 세로줄은 벽으로 설정
_tile[y][x] = TileType::WALL;
else
_tile[y][x] = TileType::EMPTY;
}
}
map<Pos, vector<CostEdge>> edges;
// edges 후보를 랜덤으로 등록
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{
if (x % 2 == 0 || y % 2 == 0)
continue;
// 우측으로 연결하는 간선 후보들
if (x < _size - 2)
{
const int32 randValue = ::rand() % 100;
Pos u = Pos{ y, x };
Pos v = Pos{ y, x + 2 };
edges[u].push_back(CostEdge{ randValue, v });
edges[v].push_back(CostEdge{ randValue, u });
}
// 아래로 연결하는 간선 후보들
if (y < _size - 2)
{
const int32 randValue = ::rand() % 100;
const int32 randValue = ::rand() % 100;
Pos u = Pos{ y, x };
Pos v = Pos{ y + 2, x };
edges[u].push_back(CostEdge{ randValue, v });
edges[v].push_back(CostEdge{ randValue, u });
}
}
}
// 해당 정점이 트리에 포함되었는가?
map<Pos, bool> added;
// 어떤 정점이 누구에 의해 연결되었는가?
map<Pos, Pos> parent;
// 만들고 있는 트리에 인접한 간선 중 해당 정점에 닿는 최소 간선의 값
map<Pos, int32> best;
// 다익스트라와 다른점은 best는 시작점 기준이 아니라는 것임(현재 트리 기준)
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{ // 초기화
best[Pos{ y,x }] = INT32_MAX;
added[Pos{ y,x }] = false;
}
}
priority_queue<CostEdge> pq;
const Pos startPos = Pos{ 1,1 };
pq.push(CostEdge{ 0,startPos });
best[startPos] = 0;
parent[startPos] = startPos;
while (pq.empty() == false)
{
CostEdge bestEdge = pq.top();
pq.pop();
// 새로 연결된 정점
Pos v = bestEdge.vtx;
// 이미 추가되었다면 스킵
if (added[v] == true)
continue;
added[v] = true;
// 맵에 적용하기
{
int y = (parent[v].y + v.y)/2;
int x = (parent[v].x + v.x)/2;
_tile[y][x] = TileType::EMPTY;
}
// 방금 추가한 정점에 인접한 간선들을 검사
for (CostEdge& edge : edges[v])
{
// 이미 해당 정점이 그룹에 추가되었다면 스킵(순환 방지)
if (added[edge.vtx] == true)
continue;
// 다른 경로로 더 좋은 후보가 발견 되었으면 스킵
if (edge.cost > best[edge.vtx])
continue;
best[edge.vtx] = edge.cost;
parent[edge.vtx] = v;
pq.push(edge);
}
}
}
(1) 기본 설정
void Board::GenerateMap_Prim()
{
struct CostEdge
{
int cost;
Pos vtx; // 좌표를 가지는 노드
bool operator<(const CostEdge& other) const
{
return cost < other.cost;
}
};
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{
if (x % 2 == 0 || y % 2 == 0) // 첫번째 가로줄과 세로줄은 벽으로 설정
_tile[y][x] = TileType::WALL;
else
_tile[y][x] = TileType::EMPTY;
}
}
}우선순위 큐를 이용하기 위해 오버로딩 된 비교 연산자에 const를 두 번 추가해준다(안하면 빌드가 안됨).
짝수번째에 벽을 만드는 코드도 그대로 사용한다.
(2) 정점과 연결된 간선 목록 관리
map<Pos, vector<CostEdge>> edges;
// edges 후보를 랜덤으로 등록
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{
if (x % 2 == 0 || y % 2 == 0)
continue;
// 우측으로 연결하는 간선 후보들
if (x < _size - 2)
{
const int32 randValue = ::rand() % 100;
Pos u = Pos{ y, x };
Pos v = Pos{ y, x + 2 };
edges[u].push_back(CostEdge{ randValue, v });
edges[v].push_back(CostEdge{ randValue, u });
}
// 아래로 연결하는 간선 후보들
if (y < _size - 2)
{
const int32 randValue = ::rand() % 100;
const int32 randValue = ::rand() % 100;
Pos u = Pos{ y, x };
Pos v = Pos{ y + 2, x };
edges[u].push_back(CostEdge{ randValue, v });
edges[v].push_back(CostEdge{ randValue, u });
}
}
}이전의 크루스칼 알고리즘에서 사용했던 코드와 유사하게 작성한다.
다만 여기서는 이중배열이 아니라 map을 사용했다.
(3) Prim 알고리즘 기본 구조
// 해당 정점이 트리에 포함되었는가?
map<Pos, bool> added;
// 어떤 정점이 누구에 의해 연결되었는가?
map<Pos, Pos> parent;
// 만들고 있는 트리에 인접한 간선 중 해당 정점에 닿는 최소 간선의 값
map<Pos, int32> best;
// 다익스트라와 다른점은 best는 시작점 기준이 아니라는 것임(현재 트리 기준)
for (int32 y = 0; y < _size; y++)
{
for (int32 x = 0; x < _size; x++)
{ // 초기화
best[Pos{ y,x }] = INT32_MAX;
added[Pos{ y,x }] = false;
}
}map을 이용해 정점이 그룹에 추가되었는지, 부모가 누구인지, 최적의 후보 값이 무엇인지 추적한다.
그리고 각 좌표를 돌면서 best 값과 added 값을 초기화한다.
(4) Prim 알고리즘
priority_queue<CostEdge> pq;
const Pos startPos = Pos{ 1,1 };
pq.push(CostEdge{ 0,startPos });
best[startPos] = 0;
parent[startPos] = startPos;최적의 경로를 찾기 위해 우선순위 큐를 사용한다.
원래 프림 알고리즘에서 시작점은 랜덤으로 선택하지만 여기에서는 시작 좌표를 점으로 선택한다.
우선순위 큐에 코스트가 0인 시작점을 넣어주고, 지금까지 발견된 최고의 값을 0으로, 시작점의 부모를 시작점으로 초기화하고 반복문을 실행한다.
while (pq.empty() == false)
{
CostEdge bestEdge = pq.top();
pq.pop();
// 새로 연결된 정점
Pos v = bestEdge.vtx;
// 이미 추가되었다면 스킵
if (added[v] == true)
continue;
added[v] = true;
// 맵에 적용하기
{
int y = (parent[v].y + v.y)/2;
int x = (parent[v].x + v.x)/2;
_tile[y][x] = TileType::EMPTY;
}
// 방금 추가한 정점에 인접한 간선들을 검사
for (CostEdge& edge : edges[v])
{
// 이미 해당 정점이 그룹에 추가되었다면 스킵(순환 방지)
if (added[edge.vtx] == true)
continue;
// 다른 경로로 더 좋은 후보가 발견 되었으면 스킵
if (edge.cost > best[edge.vtx])
continue;
best[edge.vtx] = edge.cost;
parent[edge.vtx] = v;
pq.push(edge);
}
}
}여기에서 bestEdge를 사용하여 우선순위 큐의 가장 위의 값을 받아 최소 가중치 간선을 찾는다.
(우선순위 큐는 가장 낮은 값이 위로 온다)
그리고 Pos 형 v에 최소 가중치 간선에 연결된 정점의 좌표를 저장한다.
이미 연결된 상태이면 함수를 빠져나오고, 그렇지 않다면 연결된 상태로 표시한다.
이후에 각 정점사이의 벽을 뚫어주는 코드를 Kruskal과 비슷하게 만들어준다. 다만 여기에서는 parent와 해당 정점 사이의 벽을 뚫는 방식이다.
각 정점의 간선들을 검사하여 edge.vtx 정점에 연결되는 간선의 최소 가중치를 best에 저장한다.
(이 간선은 최소 가중치 간선이다)
해당 정점의 부모를 새로 연결된 정점으로 설정하고, 이 간선을 큐에 밀어넣어 경로를 완성한다.
'자료구조와 알고리즘 > 예제' 카테고리의 다른 글
| 6-3. 크루스칼 알고리즘을 활용한 미로 맵 만들기 (0) | 2023.07.25 |
|---|---|
| 3-4. A*(A-Star) 알고리즘 (0) | 2023.07.11 |
| 3-3. 우선순위 큐 구현 연습 (0) | 2023.07.10 |
| 2-4. BFS를 이용한 길 찾기 구현 (0) | 2023.07.07 |
| 1-2. 미로 만들기(2) - 오른손 법칙(우수법) (0) | 2023.06.27 |

