3-2. 힙 트리(Heap Tree)

0. 이진 트리(Binary Tree)

각 노드가 최대 두 개의 자식 노드를 가지는 트리

위의 두 조건을 거치면 특정 값을 찾을 수 있다.

왼쪽 혹은 오른쪽으로 진행할 때 검색할 필요가 없는 나머지 부분은 날려버리고(메모리 절약) 검색을 수행한다.

그리고 각 숫자를 한쪽으로만 추가하면 균형이 깨지므로 트리 재배치로 균형을 유지하는 것이 중요하다.

 

1. 힙 트리의 특징

(1) 부모 노드의 값은 항상 자식 노드의 값보다 커야 한다

- 형제 노드 간 어떤 규칙도 만족할 필요가 없다.

 

(2) 노드 개수를 알면 트리 구조를 정확히 확정할 수 있다

- 완전 이진 트리 ; 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차 있어야 한다.

- 마지막 레벨에 노드가 있을 때에는 반드시 왼쪽부터 순서대로 채워야 한다.

=> 이 특징을 이용하여 배열을 통해 힙 구조를 표현할 수 있다.

 

1) i 번 노드의 왼쪽 자식은 (2 * i) + 1 번 노드이다. => 홀수

2) i 번 노드의 오른쪽 자식은 (2 * i) + 2 번 노드이다. => 짝수

3) i 번 노드의 부모는 [(i - 1) / 2] 번 노드이다.

(C++ 특징 상 '소수점 버림')

 

2. 힙 트리에 데이터 추가하기

'31'의 데이터를 가지는 노드를 추가하려면 세 조건을 만족해야 한다.

- 트리는 왼쪽부터 채운다

- 완전 이진 트리의 형태로 만든다

- 부모 노드가 가진 값은 항상 자식 노드의 값보다 커야한다.

(1) 해당 노드는 14의 자식 노드로 들어간다.

(2) 세번째 조건을 만족하기 위해 14와 31의 데이터를 서로 교환한다.

(3) 세번째 조건을 만족하기 위해 26과 31의 데이터를 서로 교환한다.

(4) 세번째 조건이 만족되었으므로 1번 노드('31')는 0번 노드('32')의 자식으로 남는다.

 

3. 힙 트리의 최대값 꺼내기

힙 트리의 특성에 의해 최대값은 항상 루트 노드의 값이다.

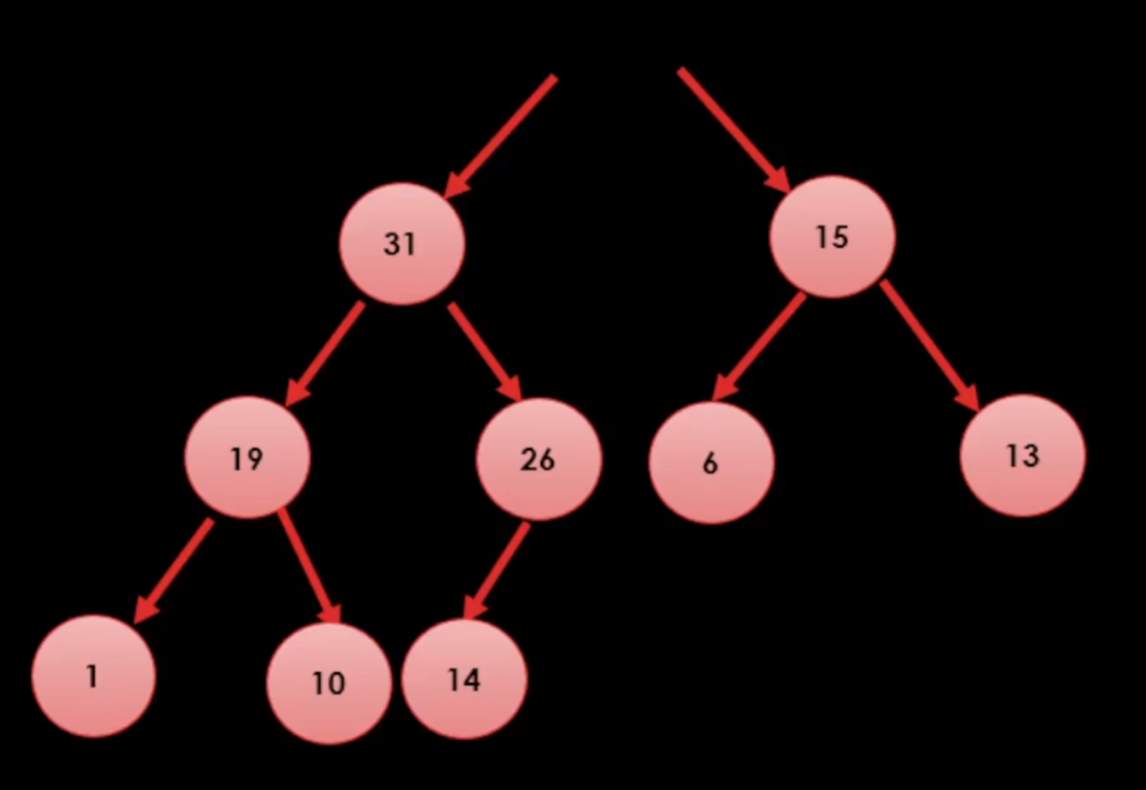
(1) 최대값을 먼저 제거한다.

(2) 제일 마지막 레벨에 위치한 데이터('14')를 루트로 옮긴다.

(3) 부모 노드의 값이 항상 자식 노드의 값보다 커야한다는 조건에 의해 자식 노드('31', '15')를 비교하여 더 큰 값('31')과 자신('14')을 비교한다.

(4) 더 큰 값이 부모 노드가 되고, 작은 값이 자식 노드가 된다.

(5) 3번과 4번을 반복하여 '14'를 가장 아래로 내려오게 만든다.

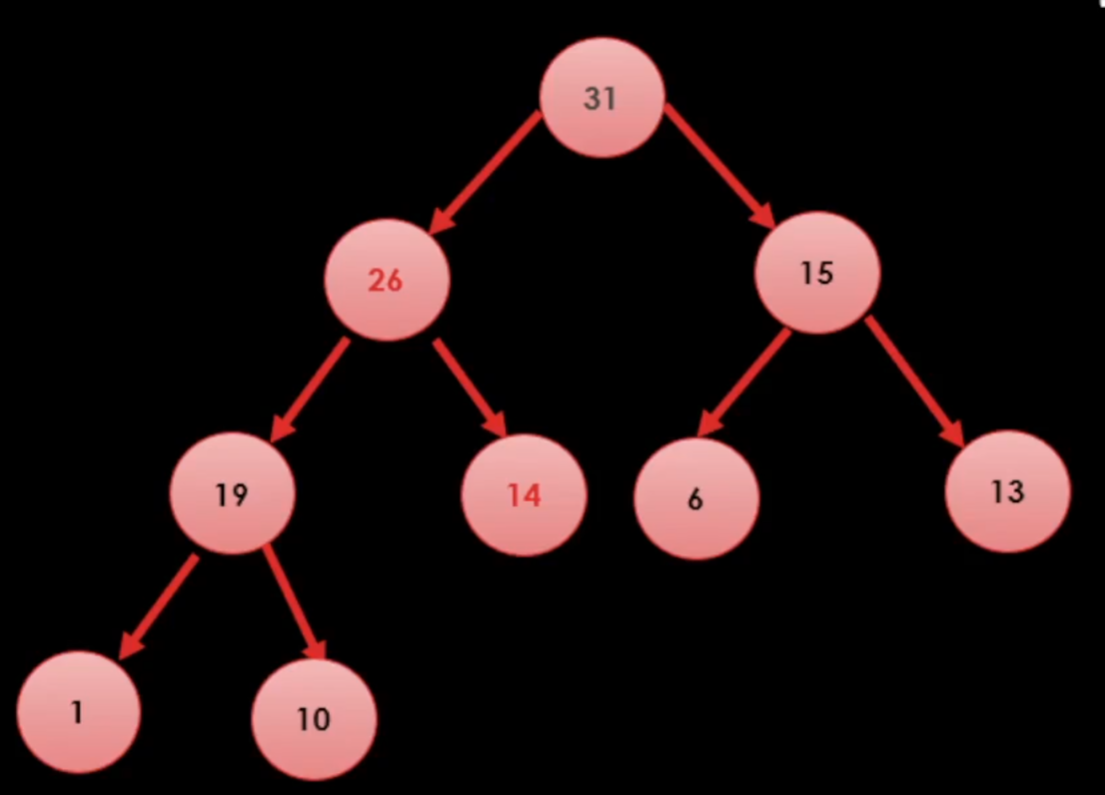
비교 후 쓸모 없는 데이터인 절반을 날리기 때문에 시간 복잡도가 O( log N )으로 list, O ( N )에 비해 빠르다.